viernes, 25 de septiembre de 2009

viernes, 18 de septiembre de 2009

Ejercicios Reduccion Gauss Jordan

2.4 Métodos de Solucion de un S.E.L.(Gauss-Jordan,Eliminacion Gaussiana)

2.3 Interpretacion Geometrica de las soluciones

2.1 Definicion de S.E.L. , 2.2 Clasificacion S.E.L y tipos de solucion

viernes, 11 de septiembre de 2009

Una matriz es un arreglo de los coeficientes constantes de un sistema de ecuaciones lineales.Para el acomodo de dichos coeficientes se toma como filas y columnas, y las coordenadas o lugares donde se encuentran cada cantidad se empiezan a numerar desde 1,1 o sea, fila 1, columna 1.Las matrices pueden ser cuadradas o rectangulares, son cuadradas cuando el numero de filas y columnas es el mismo, y son rectangulares cuando son diferentes.
Suma de matrices
La unica regla que hay para la suma de matrices es que ambas tienen que tener el mismo numero de filas y de columnas, y no importa si son rectangulares o cuadradas.Lo que se hace es sumar cada posicion de una matriz con la misma de la otra, por lo que la matriz resultante es una con el mismo numero de filas y columnas que las demas y cuyos valores son la suma de los valore de las otras 2 matrices.Por ejemplo:
=
+
Como se puede ver, la matriz resultante tiene en su posicion 1,1 la suma de la posicion 1,1 de la primera matriz mas la 1,1 de la segunda, y asi se van poniendo todas las sumas de las posiciones, y es todo lo que hay que decir acerca de la suma de matrices.
Resta de matrices
La unica regla que hay para la resta de matrices es que ambas tienen que tener el mismo numero de filas y de columnas, y no importa si son rectangulares o cuadradas.Lo que se hace es restar cada posicion de una matriz con la misma de la otra, por lo que la matriz resultante es una con el mismo numero de filas y columnas que las demas y cuyos valores son la resta de los valore de las otras 2 matrices.Por ejemplo:
=
-
El proceso es identico al de la suma, solo que aqui se restan las posiciones, por eso la matriz resultante en su posicion 1,1 tiene la resta de la posicion 1,1 de la primer matriz menos la 1,1 de la segunda.
Multiplicacion de matrices
La multiplicacion de matrices es un poco mas complicada.La regla aqui es que el numero de columnas de la primera matriz sea igual al numero de filas de la segunda, esto es, que se puede hacer una multiplicacion de una matriz 2x3 por una de 3x5, y la matriz resultante tiene el numero de filas de la primer matriz y las columnas de la segunda, por lo que quedaria una matriz de 2x5.Ademas, a diferencia de la suma y la resta, la multiplicacion no es posicion por posicion, sino que se hace de la siguiente manera:Se toma la primera fila de la primer matriz y la primer columna de la segunda matriz, y lo que se hace es multiplicar una posicion de fila por una de columna:
=
X
En el ejemplo de arriba se multiplica una matriz de 2x3 por una de 3x1, y se toma la primera fila de la primer matriz, o sea 2,4,6 y la primer columna de la otra, o sea -5,-7,6, y la resultante toma las filas de la primera, o sea 2 y las columnas de la segunda, o sea 1, y quedan 2 lugares solamente.Se llenan haciendo la multiplicacion (2x-5) + (4x-7) + (6*6) o sea posicion de fila por posicion de columna.Despues si la segunda matriz tuviera mas columnas, se pasa a la siguiente, y sin cambiar de fila en la primera se vuelve a hacer la multiplicacion y las sumas hasta que se acaben las columnas de la segunda matriz.Ya que se acabaron las filas de la segunda, se pasa a la siguiente fila en la primera y se empieza de nuevo: (-1x-5) + (3x-7) + (9x6) y se pone en el segundo lugar de la matriz, en este caso el unico que queda, pero si hubiera mas columnas se va llenando hasta que se completen las columnas y luego se baja a la siguiente fila.Asi se sigue hasta que se acaben las filas de la primer matriz.

jueves, 10 de septiembre de 2009

propiedade de numeros complejos

Números Complejos

Los Números Complejos surgen al resolver ecuaciones algebraicas en las que hay que calcular raíces cuadradas de números negativos.

Algo parecido les ocurrió a los pitagóricos al intentar medir la diagonal de un cuadrado de lado 1, se dieron cuenta que no había ningún número (sólo conocían los números naturales y fraccionarios) que midiese la diagonal. Esto dio origen a los números reales.

Representación Grafica de un Numero Complejo

Los números naturales, enteros, fraccionarios y reales se pueden representar como

puntos de una recta (la recta de los números reales).

Los Números Complejos podemos imaginarlos como puntos de un plano (el plano de los números complejos). En ese plano podemos trazar unos ejes perpendiculares que nos sirvan de referencia para localizar los puntos del plano.

Lo habitual es utilizar las coordenadas del punto (x,y). Cuando representamos un número complejo de esta forma decimos que está en forma cartesiana.

Esta interpretación de los números complejos (considerarlos puntos en un plano) se debe a Gauss y a Hamilton.

También se suele utilizar un vector para localizar el punto.

En un vector con principio en el origen de coordenadas y fin en el punto, identifica el punto de una manera inequívoca.

Al extremo del vector se le llama Afijo del complejo.

Ese vector lo podemos descomponer en dos vectores: un vector con principio en el origen de coordenadas y fin el valor de la abscisa del punto (x,y), y otro vector con principio el origen de coordenadas y fin la ordenada del punto (x,y).

Entonces el punto se representaría como una suma de vectores a + b.

Si definimos unos vectores unitarios sobre el Eje X o Real, ya que en el representamos la Parte Real del número complejo y sobre el eje Y o Eje Imaginario, representamos la parte Imaginaria. Entonces podemos representar el número de esta forma xr + yi.

Los vectores r e i tienen módulo 1, además el vector i se define cumpliendo esta condición: i2 = -1.

Cómo r tiene módulo 1 y sus potencias también son 1, no se escribe, quedando por lo tanto el número en la forma x + yi. Esta forma de representar un número complejo se llama Forma Binaria.

Conjugado de un Numero Complejo

Se llama conjugado de un número complejo al número complejo que se obtiene por simetría del dado respecto del eje de abscisas.

Representando el número complejo a + bi y haciendo la correspondiente simetría, se tiene que su conjugado es a - bi .

Dado un número complejo, su conjugado puede representarse poniendo encima del mismo una línea horizontal.

Dado un número complejo (x,y) el complejo conjugado sería (x,-y).

Si al número complejo lo representamos por n; n = (x ,y) el complejo conjugado se representa por n; n = (x ,-y) con una raya encima del número.

Propiedades de los Conjugados

· Primera propiedad

El conjugado del conjugado de un complejo z es el propio z.

Demostración:

si z = a + bi se tiene que = a - bi , de donde, = a + bi = z

· Segunda propiedad

Dados dos números complejos cualesquiera z y z' , el conjugado de su suma es igual a la suma de sus conjugados.

Demostración:

Tomando : z = a + bi y z' = c + di

Se obtiene:

a + bi y ' = c - di

Con lo que:

(a + bi ) + (c - di ) = (a + c) + (-b - d)i

· Tercera propiedad

El conjugado del producto de dos números complejos es igual al producto de los conjugados de dichos números:

Demostración:

Si z = a + bi y z = c + di

Se tiene que z · z = (ac - bd ) + (ad + bc)i

Cuyo conjugado es (ac - bd) - (ad + bc)i .

Calculando por otro lado el producto de los conjugados, resulta que

(a - bi )( c - di ) = ( ac - bd ) + ( -ad - bc) i .

· Cuarta propiedad

Los complejos que coinciden con sus conjugados son los números reales.

Demostración:

Sea un complejo a + bi que coincida con su conjugado.

Esto equivale a que:

a + bi = a - bi

Pero esto sólo ocurre si b = 0, es decir si a + bi es un número real.

· Quinta propiedad

La suma y el producto de un complejo y su conjugado son, ambos, números reales.

Demostración: (a + bi ) + (a - bi ) = 2a

(a + bi ) (a - bi ) = a2 - (bi )2 = a2 + b2

http://html.rincondelvago.com/numeros-complejos_5.html

Diagrama de Argand y Fórmula de Euler

Diagrama de Argand

Otro nombre para el plano complejo. En un sistema de coordenadas Cartesianas, un punto se puede representar usando coordenadas (x, y). Cuando este punto se toma para representar el número complejo (x+iy), al plano se le llama plano complejo, o diagrama de Argand. Se llama así en honor del matemático suizo Jean Robert Argand, una de varias personas que inventó esta representación geométrica de los números complejos.

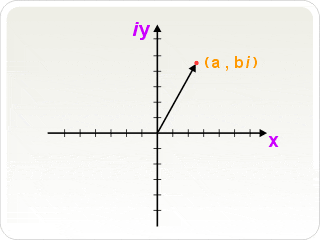
http://www.mathematicsdictionary.com/spanish/vmd/full/a/arganddiagram.htm

Fórmula de Euler

La fórmula o relación de Euler, atribuida a Leonhard Euler, establece que:

$e^{i x} = \cos x + i\,\mbox{sen}\,x$

para todo número real x. Aquí, e es la base del logaritmo natural, i es la unidad imaginaria y $senx$ y $cosx$ son funciones trigonométricas.

Esta función tiene, tanto simetría par como impar sabido que este tipo de simetrías desempeñan un papel muy importante en la física moderna, razón por la cual en la mecánica cuántica los números complejos son esenciales.

http://es.wikipedia.org/wiki/F%C3%B3rmula_de_Euler

diferencia de cubos

1.6 ECUACIONES POLINOMICAS

Una ecuación es una igualdad entre dos expresiones algebraicas, denominadas miembros, en las que aparecen valores conocidos o datos, y desconocidos o incógnitas, relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser números, coeficientes o constantes; y también variables cuya magnitud se haya establecido como resultado de otras operaciones. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar. Por ejemplo, en la ecuación:

$\overbrace{3x-1}^{\text{primer miembro}}=\overbrace{9+x}^{\text{segundo miembro}}$

La letra x representa la incógnita, mientras que el coeficiente 3 y los números 1 y 9 son constantes conocidas. Resolver una ecuación es encontrar los valores de las incógnitas que la satisfacen, y se llama solución de una ecuación a cualquier valor de dichas variables que cumpla la igualdad planteada. Para el caso dado, la solución es:

$x = 5 \,$

Todo problema matemático puede expresarse en forma de una o más ecuaciones. Sin embargo no todas las ecuaciones tienen solución, ya que es posible que no exista ningún valor de la incógnita que haga cierta una dada igualdad. También puede ocurrir que haya varios o incluso infinitos conjuntos de valores que la satisfagan.

En el caso que todo valor posible de la incógnita haga cumplir la igualdad, la expresión se llama identidad. Si en lugar de una igualdad se trata de una desigualdad entre dos expresiones matemáticas, se denominará inecuación. Una ecuación funcional es aquella en la que algunas de las constantes y variables que intervienen no son realmente números sino funciones; y si en la ecuación aparece algún operador diferencial se llama ecuación diferencial.

Ecuación polinómica

Una ecuación polinómica es una igualdad entre dos polinomios. Realizando las mismas transformaciones y en el mismo orden, en los dos miembros de la ecuación, puede conseguirse que uno de ellos se reduzca a cero, razón por la cual se suele considerar que una ecuación polinómica es aquella que en el primer miembro aparece un polinomio y en el segundo aparece el cero. Ejemplo:

$x^3y+4x-y=-2xy \,\!$